Predator - prey interactions
Introduction
In the Lotka-Voterra common resource competition exercise, we saw that the dynamics of any given species can be influenced by those of other species which are competing with it for resources. This often takes place within a particular trophic level. Two species of ungulates could feed on grasslands within a common area, for instance. In nature, population dynamics are also regulated by species across trophic levels – the dynamics of predator populations are influenced by how many prey individuals are in the community is a common example of this. These predator-prey interactions are also described by Lotka-Voterra equations. In this case these are a pair of differential equations describing the population dynamics of one species at one trophic level as a function of the dynamics of species within another other trophic level. Although it is most commonly discussed in a “predator-prey” context, the framework here can me modified to suit other scenarios such as plant-herbivore, parasites-host interactions.
Exponentially growing prey
Due to the greater complexity of the relationships involved when modelling two species interactions we will not be using derrived equations. Rather we will use the differential equation as our model. We will be using the deSolve package to help us solve these differential equations which we will then plot as normal.
The simplest Lotka-Volterra predator-prey equation considers a prey or victim species \(V\) that grows exponentially at a rate \(r\), and shrinks as it gets consumed by predators \(P\), which attack the prey they encounter at a fixed, per-capita (i.e. dependent on the number of predators and prey) rate \(\alpha\):
\[\frac{dV}{dt} = rV - \alpha VP\]
The population of the predators \(P\) grows as it converts the prey which it encountered and consumed into new predator individuals at a fixed per-captia rate \(\beta\), and shrinks due to a constant per-capita mortality rate \(d\):
\[\frac{dP}{dt} = \beta \alpha VP - dP\]
Let’s take a look at what this model implies. When there are no predators in the community (i.e. \(P = 0\)), the prey species \(V\) grows due to simple exponential growth (\(rV\)). If there were limiting resources then the prey would grow until its carrying capacity but we will ignore that aspect in this example for simplicity. Conversely, when there are no prey individuals in the community (i.e. \(V = 0\)), the predator popultion has no way to sustain its growth grow and exponentially declines towards zero \(-dP\).
The rate of growth of the predator population increases when prey are abundant and predators are few. On the other hand, when there are plenty of predators, the prey population suffers and cannot grow very quickly. We can get some suggestion that this predator-prey relationship might lead to some sort of population cycling – as the prey population grows, so too does the predator popuplation, which in turn reduced the number of prey which in turn reduces the number of predators allowing the prey to increase once more.
As expected, cyclic population dynamics are common in predator-prey systems:
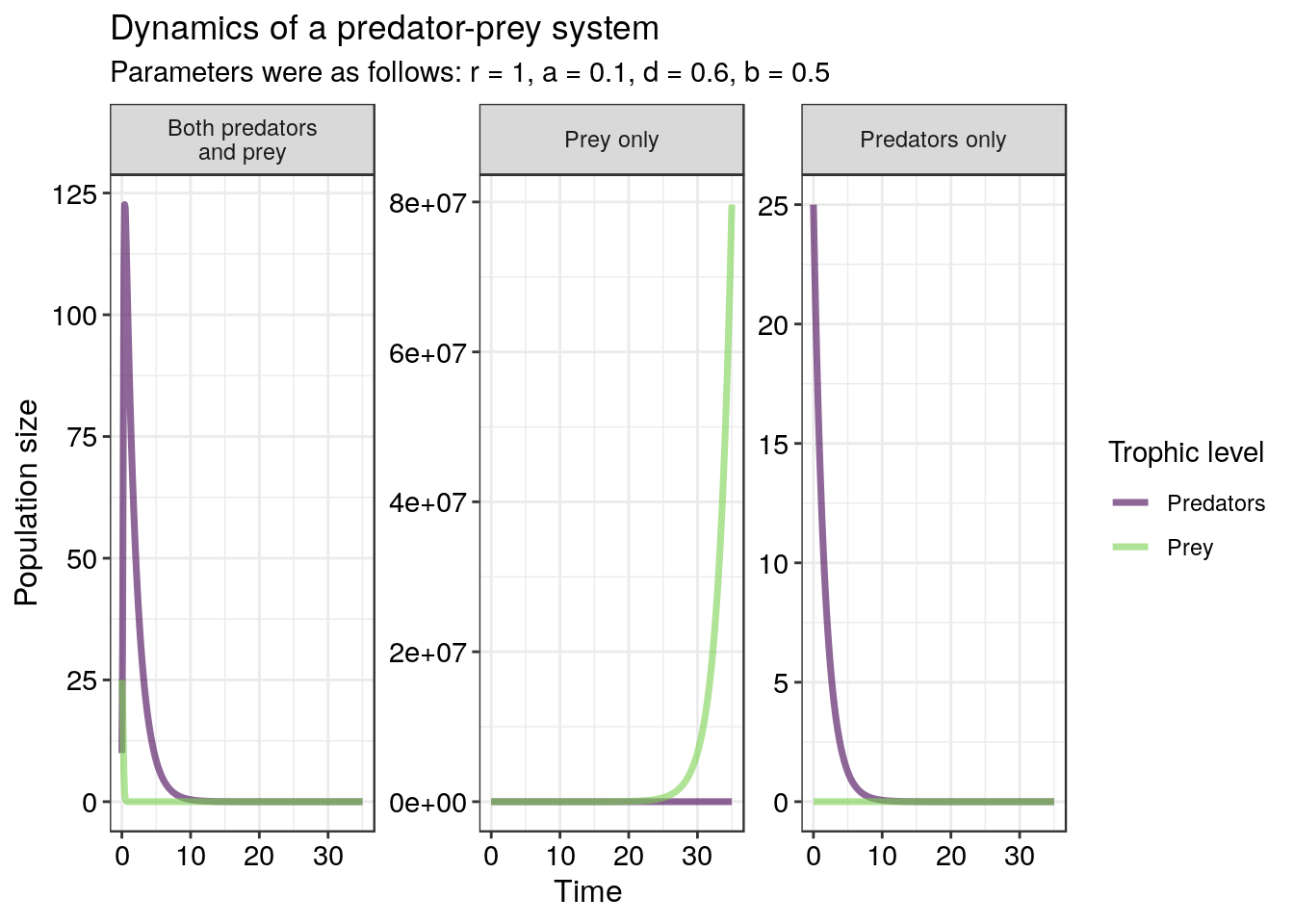
In the first plot above, the system begins with 25 prey and 10 predators – cyclic dynamics shortly ensue. In the middle panel, there are no predators in the beginning, so the prey population simply grows exponentially. In the third panel, there are no prey individuals in the system – so, the predator population shrinks exponentially to zero.
Logistically growing prey
In the previous model, prey experience exponential growth when predators are absent – in other words, the predators are the only factor regulating the prey population’s dynamics. Of course, this doesn’t generally happen in nature. Even when predators are absent a prey population will eventually level off at some carrying capacity dictated by the available resources within the habitat.
To incorporate this aspect into our equations we can modify the above prey equation by incorporating density-dependent growth simply by adding a term to represent the population’s carrying capacity:
\[\frac{dV}{dt} = rV - \alpha VP - cV^2\]
Where the value of the carrying capacity can be calculated as \(K = \frac{r}{c}\) which has been taken from logistic population growth. So if you want a very large \(K\) then make \(c\) very small. We keep the predator population dynamics the same as before:
\[\frac{dP}{dt} = baNP - dP\]
With these new equations, when predators are absent from the community, the prey species grows exponentially but it is then restricted by its own abundance in a similar manner to how the logistic growth equation would function. One possible outcome in this case is stabilised population cycles - in other words, the predator and prey populations can cycle up and down until they reach a joint equilibrium:
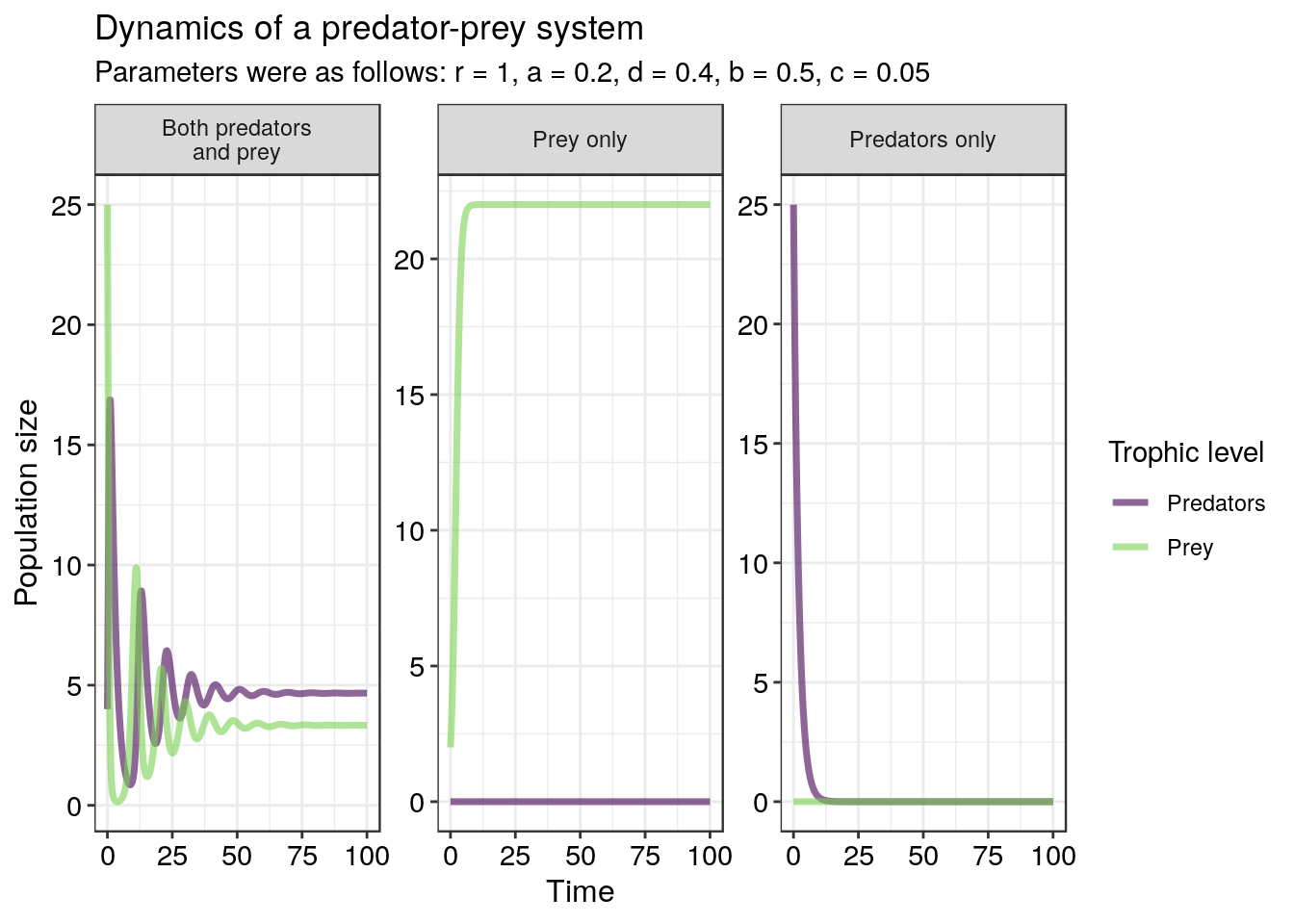
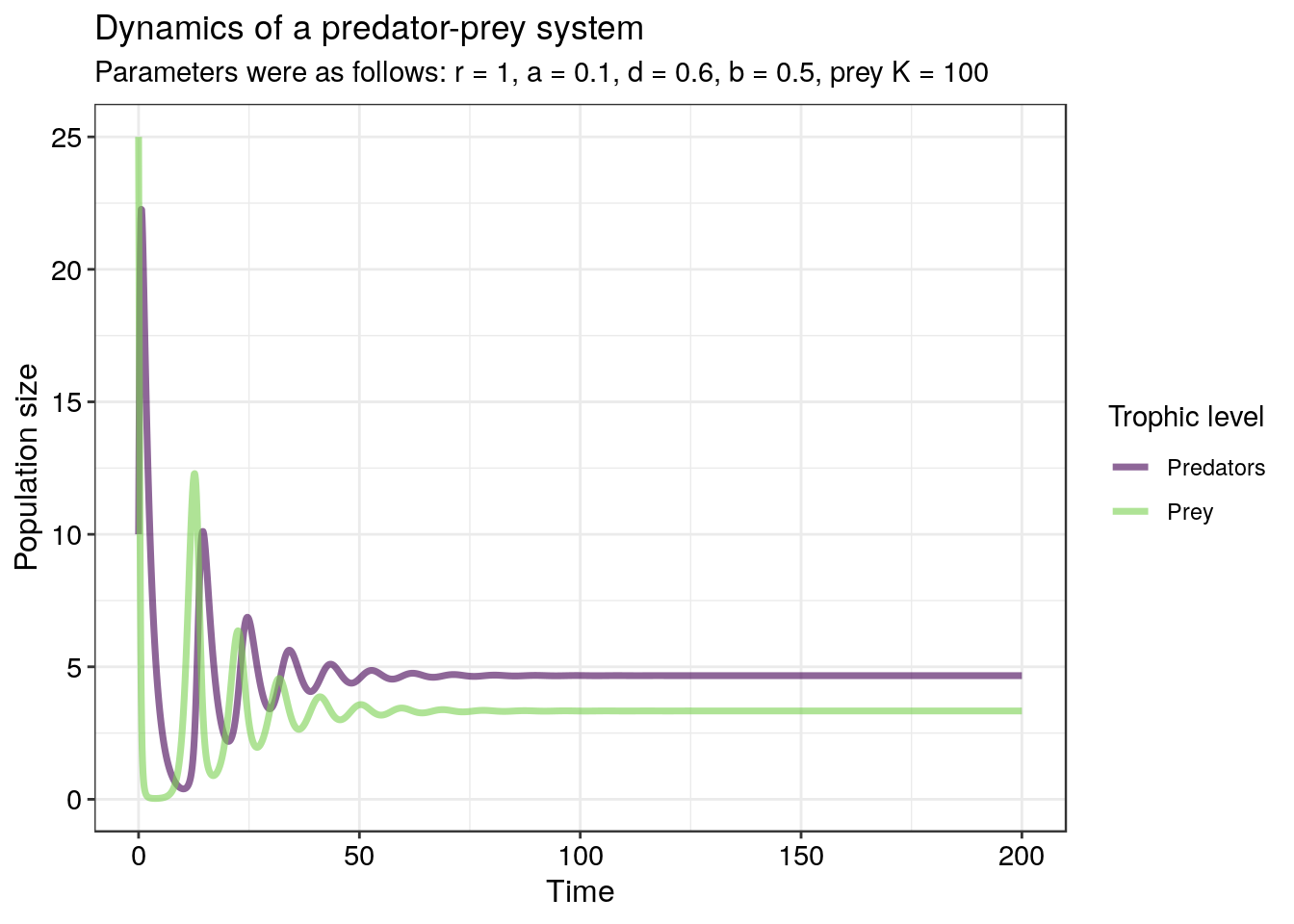
Note that in the middle graph, the prey population grows logistically to its carrying capacity of 10 when no predators are present. If we run this system out longer, we see that the populations eventually stop cycling as they reach an equilibrium when both predator and prey are present in the system:
Parameter exploration
Download Lotka-Voltera predator prey app here and answer the questions on the prac worksheet.
This app requires several parameters and the user interface is quite cluttered. The default app viewer which you have likely been using for the previous apps will not work well and it will be better for you to run the app in your web browser. To do this run the app file from RStudio and then click Open in browser. Once open in your web browser do not close the app file as this will crash the browser page. To see all the app options in the browser app you will need to zoom out to approximately 80%.
Worksheet questions (30)
Question 1
An important starting point for any model is understanding what the different aspects of the equation represent. One can access this information from the units that a particular parameter is measured or reported in. Give the units of:
- \(\alpha\) (3)
- \(\beta\) (3)
Question 2
Briefly explain how the term \(cV^2\) produces similar outcomes to the term \(\left(1-\frac{N}{K}\right)\) which we have used in the exponential and logistic growth practical (3)
Why do we only incorporate carrying capacity (in the form \(\left(\frac{r}{c}\right)\) in today’s example) into the prey population growth equation but not into the predator population growth equation (2)
Question 3
Which model parameters influence the magnitude and frequency/periodicity of the fluctuations of the predator and prey populations when there is no carrying capacity (4)
Question 4
Both the incorporation and exclusion of carrying capacity results in the populations reaching some kind of equilibrium. This equilibrium can be stable or unstable. Describe how the parameters of the predator and prey populations interact with each other as the populations approach this equilibrium and state the kind of equilibrium reached
- without a prey carrying capacity (4)
- with a prey carrying capacity (4)
Make specific reference to the ZNGI curves.
Question 5
Under what conditions will the predators not be able to successfully establish themselves and thus become extinct from the community (4)
Question 6
Discuss the application of the second figure – what information does it convey and what could it be used for in a conservation/management scenario (3)
Coding questions (20)
We will be introducing a new aspect into our code in this practical. Because we have two separate equations to model it is easier for us to provide the computer with our rate of change equations and then for the computer to integrate these equations and calculate the population sizes automatically.
You may remember this being mentioned in earlier practicals but if you don’t then you’ll be glad to know that R has a fantastic package called deSolve (differential equation Solver) which is just right for the job! This package is very powerful but requires a bit of a learning curve. Understanding everything about this package is beyond the scope of these practicals but with what you have learned from the previous practicals together with a short tutorial on the package you should be able to obtain basic outputs from the package.
There are three main aspects needed for us to use deSolve successfully.
First we need to define a
function()which contains all of the aspects relating to the differential equations. In the code below this function is calledepgbecause the model it is working with is the exponential population growth model. This function takes three arguments;time,init, andparameters. The body of the code then containswith()which tells the next bit of code make use oftime,initandparametersin the next code chunk. This next bit of code is where the differential equations are stored (in our case the equation is stored asdNdt. Each equation gets stored in an appropriately named variable and then the final call in this function is toreturn()these equations. Although this function is defined at the beginning of our script it does not actually run until we callepg()and supply arguments for it. All we are doing is just defining a function just as we would any other variable.The next aspects of our code are to define the length and values of the predictor series (in our case this is
timeas asequence of numbers beginning at 0, ending at 1000, and increasing by 1), theinitial values of the population(s) we are dealing with and theparameters associated with each equation. These are the vectors that will be combined withwith()and fed into the differential equations.Our final next step is to generate
out, a variable which stores the output of theodefunction.ode()(full function name: General Solver for Ordinary Differential Equations) is the function within thedeSolvepackage which will carry out the calculations necessary to determine the changes in population sizes between the time steps. This function needs four parameters fed to it - all of which we have already:- The first argument is
y- the initial values for each of the differential equations - we would have stored these ininit
- Next we need
times, the time values we want to use to integrate these differnetials at - we have these values stored intimes
- Then we need
funcwhich is the function that contains the equations - we have developed this function and called itequ()
- And finally we need
parms, the parameters which are fed intofuncwhich we have calledparams
- The first argument is
Once we have all those inputted to ode and we have run it successfully we can simply convert the output to a data frame (using as.data.frame()) and then we can neatly plot our modified data frame using ggplot(). See the code below as an example - the three components listed as required above are also explicitly stated in the code required to produce the figure below:
# load required packages
list.of.packages <- c("deSolve", "dplyr", "ggplot2")
#checking missing packages from list
new.packages <- list.of.packages[!(list.of.packages %in% installed.packages()[,"Package"])]
#install missing ones
if(length(new.packages)) install.packages(new.packages, dependencies = TRUE)
# load packages from library
library(deSolve)
library(dplyr)
library(ggplot2)
# define function which accepts arguments for the population parameter vectors (time, init, params),
# parses these to the equation using with()
# and then returns the output
epg <- function(time, init, params) {
with (as.list(c(time, init, params)), {
dNdt <- r*N
return(list(c(dNdt)))
})
}
# define values of the parameter vectors
time <- seq(from = 0, to = 30, by = 0.1)
init <- c("N" = 1)
params <- c("r" = 0.2)
# populate a matrix called out in our case using ode() and supplying all the required arguments
out <- ode(y = init,
times = time,
func = epg,
parms = params)
# convert out to a data frame using dplyr
out <- out %>% as.data.frame()
# plot the out dataframe using ggplot2
ggplot(out) +
geom_line(aes(x = time,
y = N),
size = 1.25,
alpha = 0.6) +
labs(title = "Exponentially growing population",
subtitle = "Parameters were as follows: N0 = 1, r = 0.2",
x = "Time",
y = "Population size") +
theme_bw() +
theme(axis.title = element_text(colour = "black",
size = 12),
axis.text = element_text(colour = "black",
size = 11)) 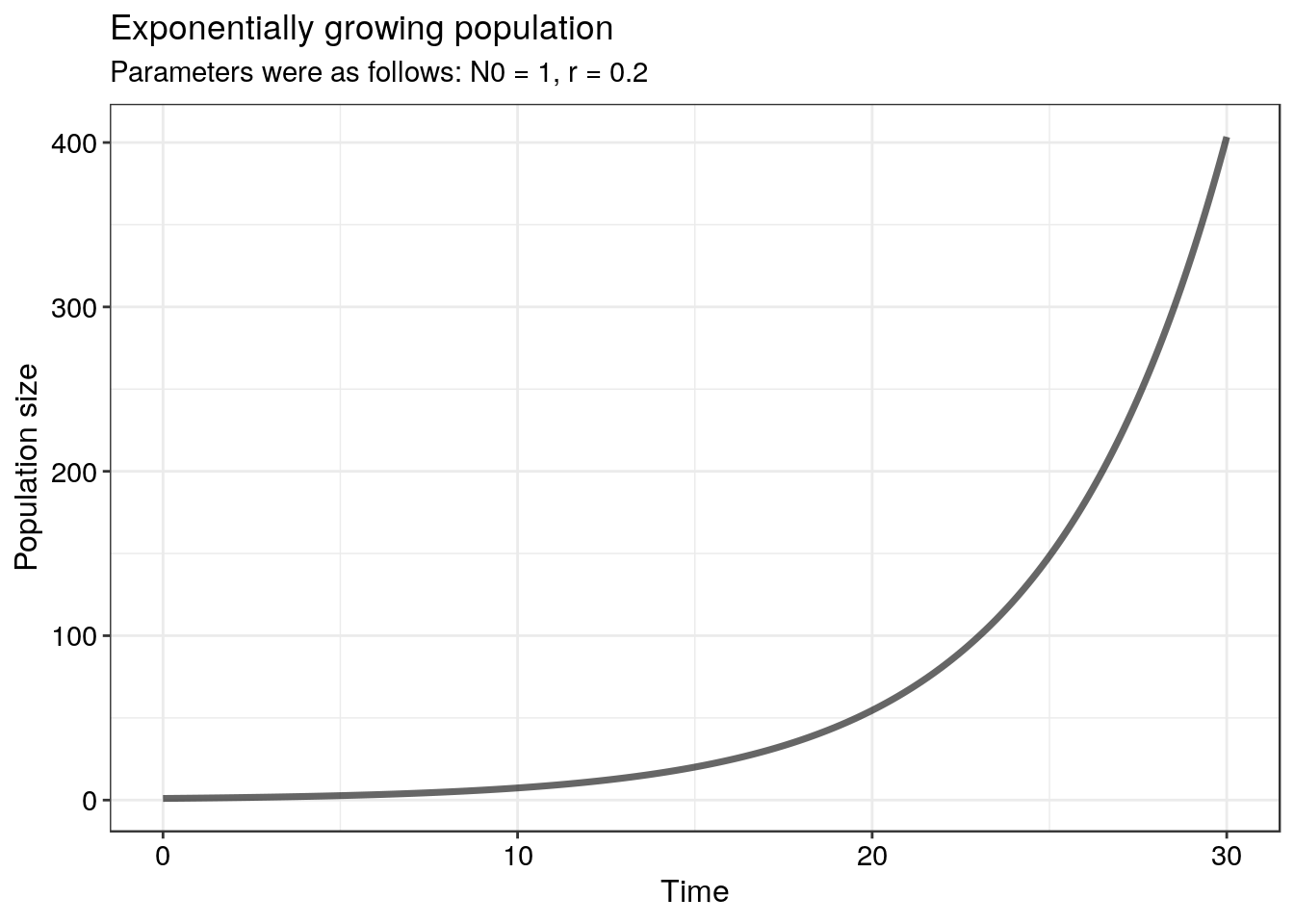
Question 1
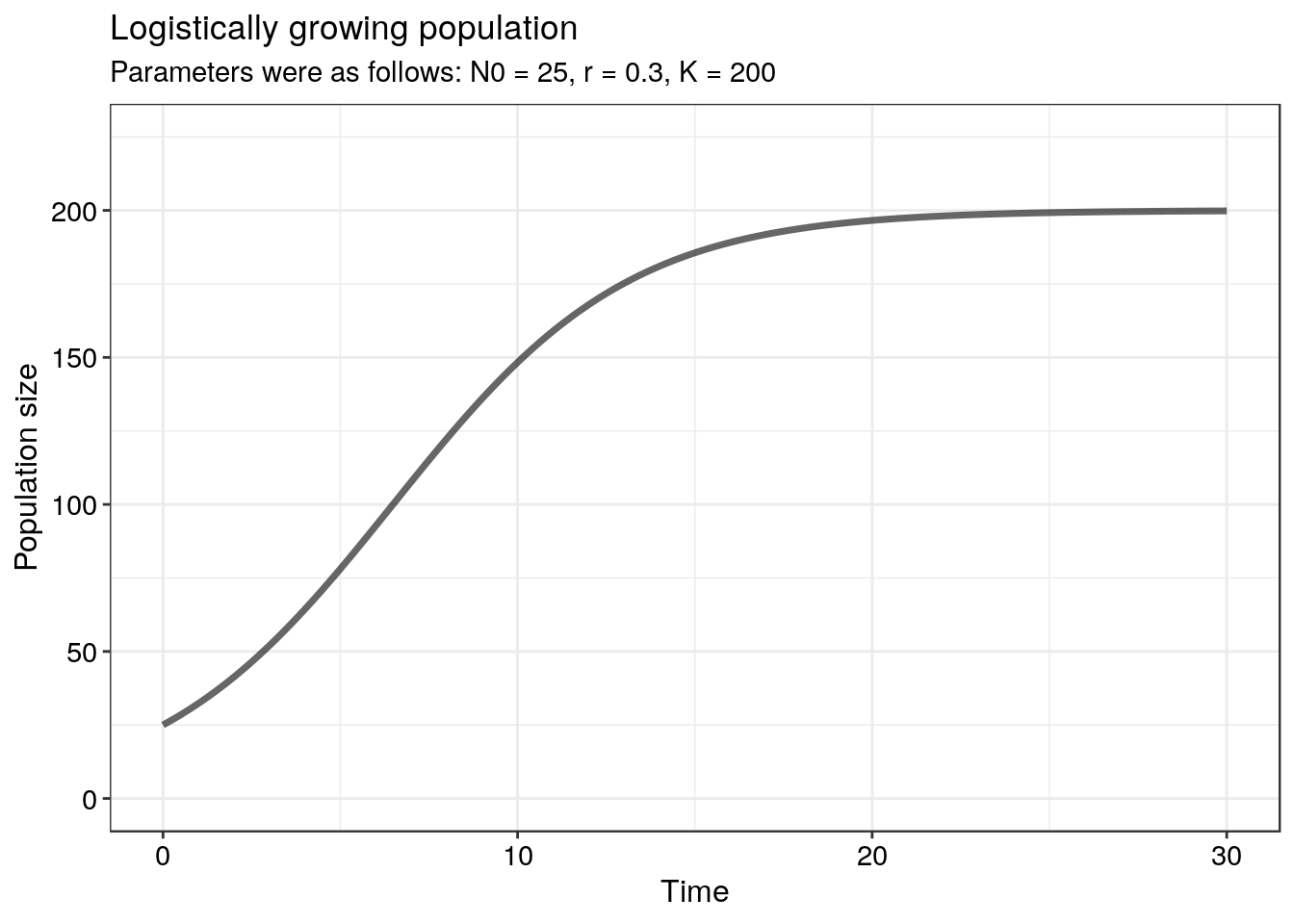
By using the code supplied above as a starting point produce a plot that resembles this output (14)
Question 2
In your own words describe the three aspects required to calculate the integrals for each time period and how they work together to produce the desired output (6)
Application questions (38)
Question 1
List and describe the assumptions of the predator-prey model with and without the prey carrying capacity (10)
Question 2
There are many other factors that can influence predator-prey models. We have looked at incorporating carrying capacity into our model. Two other sources are predator functional response types (Type I, II, or III) and prey refuges. Discuss how these two influences likely influence the output of the model (6)
Question 3
The paradox of enrichment is an important idea when managing predator-prey scenarios. Discuss what the paradox of enrichment is, which kind of species are involved in these interactions, and briefly describe how it can impact agricultural systems (8)
Question 4
Some of the more commonly studied and cited examples of predator-prey interactions concern northern hemisphere animals. However, some of the most exciting examples come from Africa. Identify one scientific articles which study predator-prey interactions in Africa. For the article supply:
- the full citation (1 mark each)
- the predator and the prey species (2 marks)
- a paragraph where five points describing the key findings of the study specifically concerning the interactions between the predators and the prey in relation to the study’s context and aims and objectives (5 marks) (total = 8)