Population Growth
Introduction
When a species is of conservation concern, we are interested in whether populations of the species can persist in the long term. In order to examine population viability (a measurement of whether a species will persist through time), we can use demographic information to model population dynamics.
Usually we start with the idea that in any population, the number of individuals at any particular time is governed by the initial population size, \(N_0\), and the number of births, deaths, immigrations, and emigarations that occur. We can describe this kind of population using the following diagram:

Given this scenario we could use the equation
\[ N_{t+1} = N_t + B - D + I - E \] to describe how the population changes between time periods. Here \(N_t\) represents the number of individuals in the population, \(B\) represents the number of births, \(D\) the number of deaths, \(I\) the number of immigrations, and \(E\) the number of emmigrations. In the simplest approach, we can use a disctrete-time model and demographic information to predict the expected size of a population over time.
The above equation has several sources of external variability due to external influences and so for simplicity we will consider a closed population, where there are no immigarants joining the population or emmigrants leaving the population. In our example only births and deaths will affect the number of inidividuals in the population.
To further simplify our model, we will not explicitly address deaths. Instead we examine suvivorship, \(S\), or the per capita probability of suriving in a particular timestep. \(S\) is still calculated with the per capita death rate (\(d\)) in mind:
\[S=1-d\] This equation means that the probability that an individual will survive (\(S\)) plus the probability that an individual will die (\(d\)) must add to one. From this we can estimate the number of individuals alive at time \(t+1\) as \(N_t \times S\). Then population size in each timestep is a function of the population size at the time before (\(N_t\)), survivorship (\(S\)), and the per capita birth rate (\(b\)) as shown in the equation below.
\[N_t+1=N_t [S+b]\]
Use the Exponential growth: Births and survivorship app to study this equation a little further. Use this app to answer the questions on the prac sheet.
Download the exponential growth: Births and deaths app here
Futhermore, in order for a population to remain viable in the long term, survivorship and births must be balanced so that \(S+b \ge 1\). The term \(\lambda\) is often used to summarize the sum of per capita survivorship and births:
\[\lambda= S+b\]
So, instead of changing \(S\) and \(b\) independently, we can use \(\lambda\) in our model to summarize the dynamics of the population. Use the Exponential growth: Lambda app to answer the next set of questions on your prac sheet.
Download the exponential growth: Lambda app here
Logistic population growth
The problem with exponential models is that they do not incorporate a ceiling - the population grows towards infinity. As you will likely see later when you answer the questions later there are very few types of organisms which we study which exhibit exponential growth patterns. What is more commonly encountered by us maro-ecologists are populations which reach what we call a “carrying capacity” - the population size at which the resources in the environment are too few to sustain the population or allow it to grow. This is the next idea we will explore today.
The equation for logistic growth is very similar to the exponential growth equation except that there is an extra term added which gives us
\[\frac{dN}{dt} = rN\frac{1-N}{K}\]
This is the derived form of the logistic equation representing the “rate of change” of the population size through time. The second part \(\left(\frac{1-N}{K}\right)\) adjusts the growth rate towards zero as \(N\) tends towards \(K\). When \(N = K\) we have \(1-1 = 0\) and so the change in population size \(\frac{dN}{dt}\) equals zero. When the population size is very far away from \(K\) the magnitude of the adjustment increases - this takes into account whether there are many resources not being used (very small \(N\)) or when too many resources are being used (very large \(N\)). As \(N\) approaches the carrying capacity the rate of change in the population size decreases. Th opposite occurs when the population size is very different to the carrying capacity. Aside from the rate of change in population size changing the direction of this change can also vary. With this equation a population size grater than K will result in a population which decreases in size until it reaches the carrying capacity.
This is a very useful equation, however, it is harder to use for producing simple plots such as the ones we are interested in for today’s practical. This is because if we plot this equation we will plot the rate of change of the population through time rather than the population size through time. To get around this problem we can integrate this equation to get
\[ N_t = \frac{K}{1 + [(\frac{K - N_0}{N_0})]e^{-rt}} \] where \(K\) is the carrying capacity, \(N_0\) is the initial population size, \(r\) is the intrinsic rate of growth of the population (birth rate minus death rate - different to \(\lambda\) which is equal to \(S + b\)) and \(t\) being time.
Let’s see this idea in action:
Download the logistic population growth app here
A bief note about calculus in population ecology and R
An important aspect of any population study is the rate of change of a population’s size between two time periods \(\left(\frac{dN}{dt}\right)\). Going back to MATH150 you’ll hopefully remember that the term for this is differentiation. Some equations are pretty easy to differentiate (a cubic function (the logisic growth equation is a variation of this) differentiates to a parabolic function) but many of the equations used in population ecology are a little more complicated than this and so differentiating more complicated equations becomes much more tricky and likely goes beyond the scope of MATh150. Fortunately for us, R has several packages which takes care of this differentiation stuff for us! One such package is deSolve. In later practicals we will learn how to use this package but for now we will just focus understanding the relationship between the variables involved in the equations rather than computing the relationship ourselves.
Worksheet questions
Exponential growth
Use the first two apps to answer the following questions
Question 1
How many years does it take for a population to go extinct when:
- \(S\) = 0.6 and \(b\) = 0.4 (1)
- \(S\) = 0.6 and \(b\) = 0.3 (1)
- \(S\) = 0.5 and \(b\) = 0.6 (1)
Question 2
What is the equivalent \(\lambda\) value for when \(S\) = 0.8 and \(b\) = 0.4? (2)
Logistic growth
Use the third app to answer the following questions.
You should see a button labelled Plot change in population growth on this app window, click it and you should now see two plots. Both these plots are plotting data from the same model, the one we have already looked at is plotting the actual population size through time while the other is plotting the rate of change of the population through time
Question 1
Describe the shape of the logistic growth plot when the model parameters are set to:
- \(N_0\) = 50, \(K\) = 100, \(r\) = -0.05 (2)
- \(N_0\) = 60, \(K\) = 50, \(r\) = 0.6 (2)
- \(N_0\) = 80, \(K\) = 60, \(r\) = 0.05 (2)
- \(N_0\) = 20, \(K\) = 70, \(r\) = 0.8 (2)
Question 2
Under what circumstances will a population go extinct given this growth model? (2)
Question 3
There is a negative sign in front of \(r\) in the exponent term. Why is that there? (3)
Question 4
Study the rate of change graph accompanying the logistic growth plot. Discuss (with reference to the model parameters) how the rate of change plot changes in relation to the logistic growth plot. (6)
Question 5
Based on your answer to Question 4 describe briefly how the per capita rate of change curve \(\frac{\frac{dN}{dt}}{dN}\) would look like plotted against time (3)
Coding questions
- The following code is mostly complete except for a few errors which result in a completely incorrect output. Identify the errors (there are four in total worth one mark each) to produce a plot that matches the one below it. You can copy this code directly into RStudio. Edit the code until it produces the desired output and then copy the corrected code into a word document. In your word document also list each of the errors and briefly (no more than one sentence) describe how you fixed the error (10)
library(ggplot2) # For loading the package required to produce the plot output
N0 <- 50 # The initial population size
years <- 30 # The number of time steps
lambda <- 1.4 # The population growth rate, lambda
N <- c(N0, rep(0, times = years - 1)) # Create an open vector for data
#Run a loop that considers each time step (t) as a function of the time step before it (t-1) and lambda
for (t in 2:years) {
N[t] <- N[t - 1]*(lambda)
}
time <- seq(from=1, to = years, by = 1) #Create a vector of time steps for plotting
plot_df <- data.frame(Size = N, Time = time)
ggplot(data = plot_df) +
geom_line(aes(x = Time, y = Size)) +
labs(x = "Time")
theme_bw() +
theme(axis.title = element_text(colour = "black",
size = 12),
axis.text = element_text(colour = "black",
size = 11),
legend.title = element_text(colour = "black",
size = 12),
legend.text = element_text(colour = "black",
size = 11))
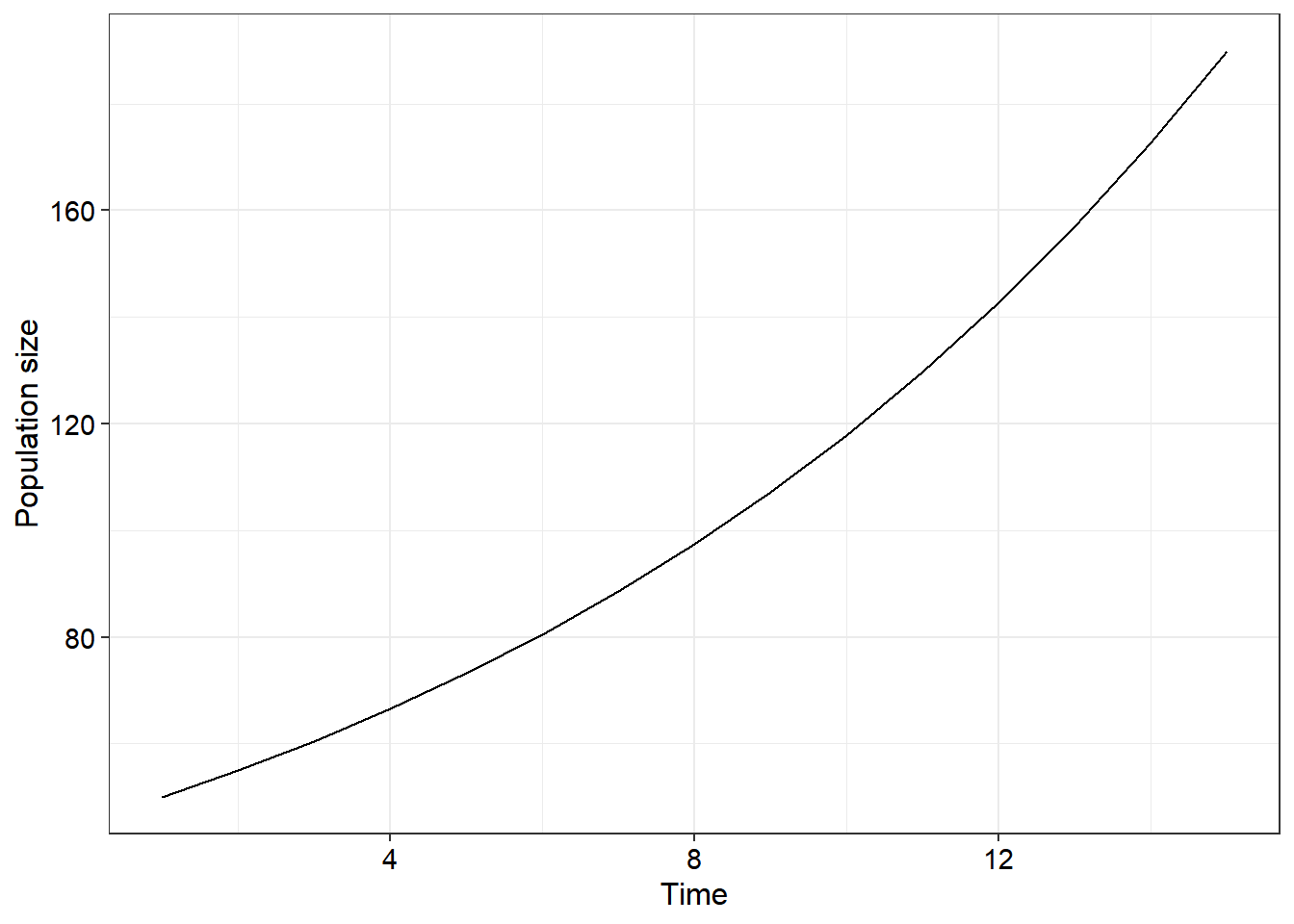
- Similar to the above scenario, the following code also contains several errors. However, there are two “fatal” errors in this scenario - that is the code does not successfully compile. Present your corrections in the same manner as described in the previous question (10)
library(ggplot2) # For loading the package required to produce the plot output
N0 <- 25 # The intitial population size
years <- 15 # The number of time steps
r <- 1.01 # The population growth rate, lambda
K <- 90
N <- rep(0, times = years+1) # Create an open vector for data
years <- seq(from = 0,
to = years,
by = 2)
for (i in 1:length(N)+1) {
N[i] <- K/(1+((K-N0)/N0)*exp(-r*years[i]))
}
ggplot() +
geom_point(aes(x = years, y = N)) +
geom_line(aes(x = years, y = N)) +
labs(x = "Years") +
theme_bw() +
theme(axis.title = element_text(colour = "black",
size = 12),
axis.text = element_text(colour = "black",
size = 11),
legend.title = element_text(colour = "black",
size = 12),
legend.text = element_text(colour = "black",
size = 11))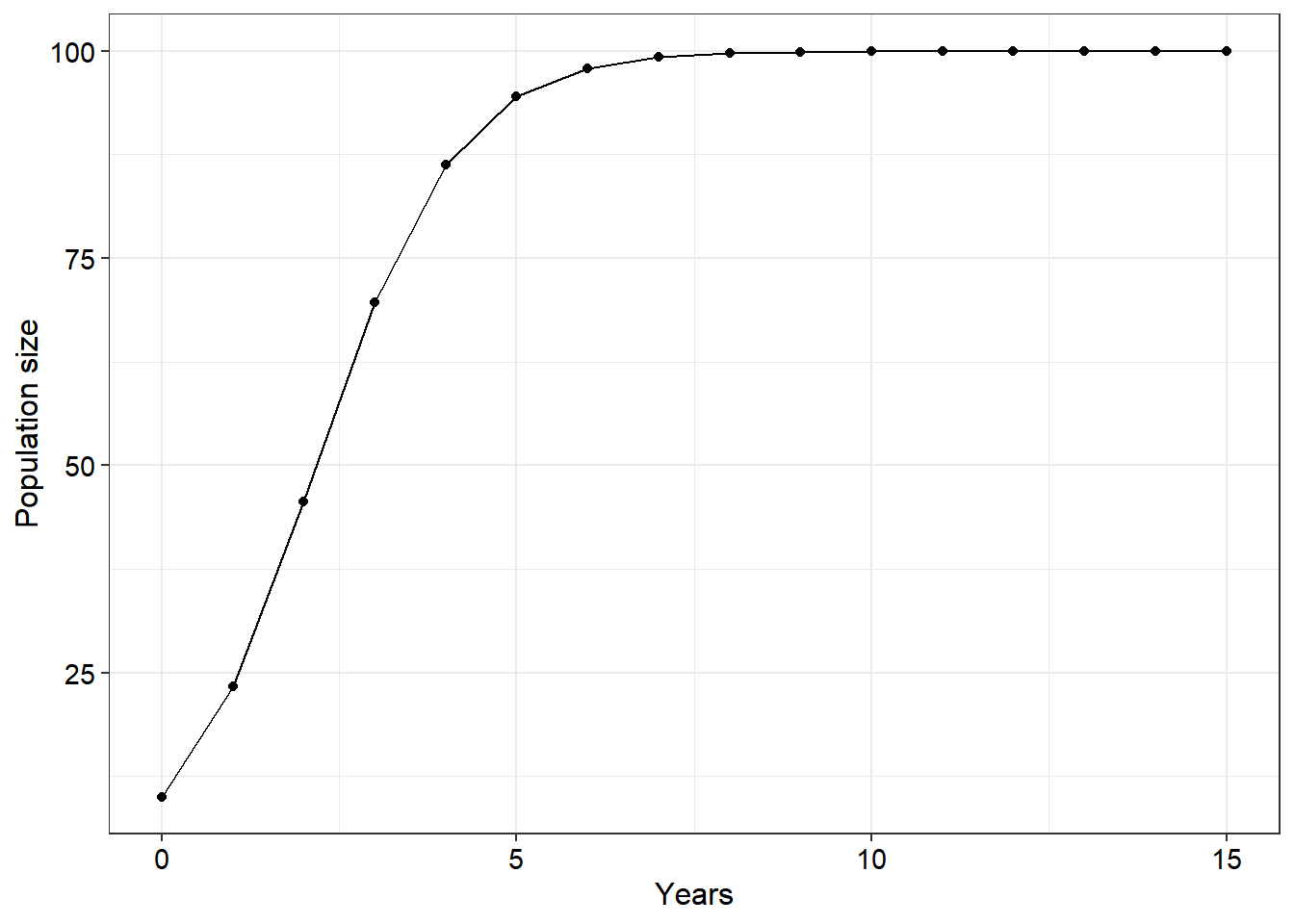
- Bonus challenge. The following plot is similar to the first plot, however, there are some important changes that need to be made to the figure output section in order to obtain the desired output. Look carefully at the output for some hints and suggestions. You will also need to include a new
geomlayer (5)
library(ggplot2) # For loading the package required to produce the plot output
N0 <- 50 # The intitial population size
years <- 30 # The number of time steps
lambda <- 1.4 # The population growth rate, lambda
N <- c(N0, rep(0, times = years - 1)) # Create an open vector for data
# Run a loop that considers each time step (t)
# as a function of the time step before it (t-1) and lambda
for (t in 2:years) {
N[t] <- N[t - 1]*(lambda)
}
time <- seq(from = 1,
to = years,
by = 1) #Create a vector of time steps for plotting
plot_df <- data.frame(Size = N, Time = time)
ggplot(plot_df) +
geom_line(aes(x = Time, y = Size)) +
labs(x = "Time")
theme_bw() +
theme(axis.title = element_text(colour = "black",
size = 12),
axis.text = element_text(colour = "black",
size = 11),
legend.title = element_text(colour = "black",
size = 12),
legend.text = element_text(colour = "black",
size = 11))
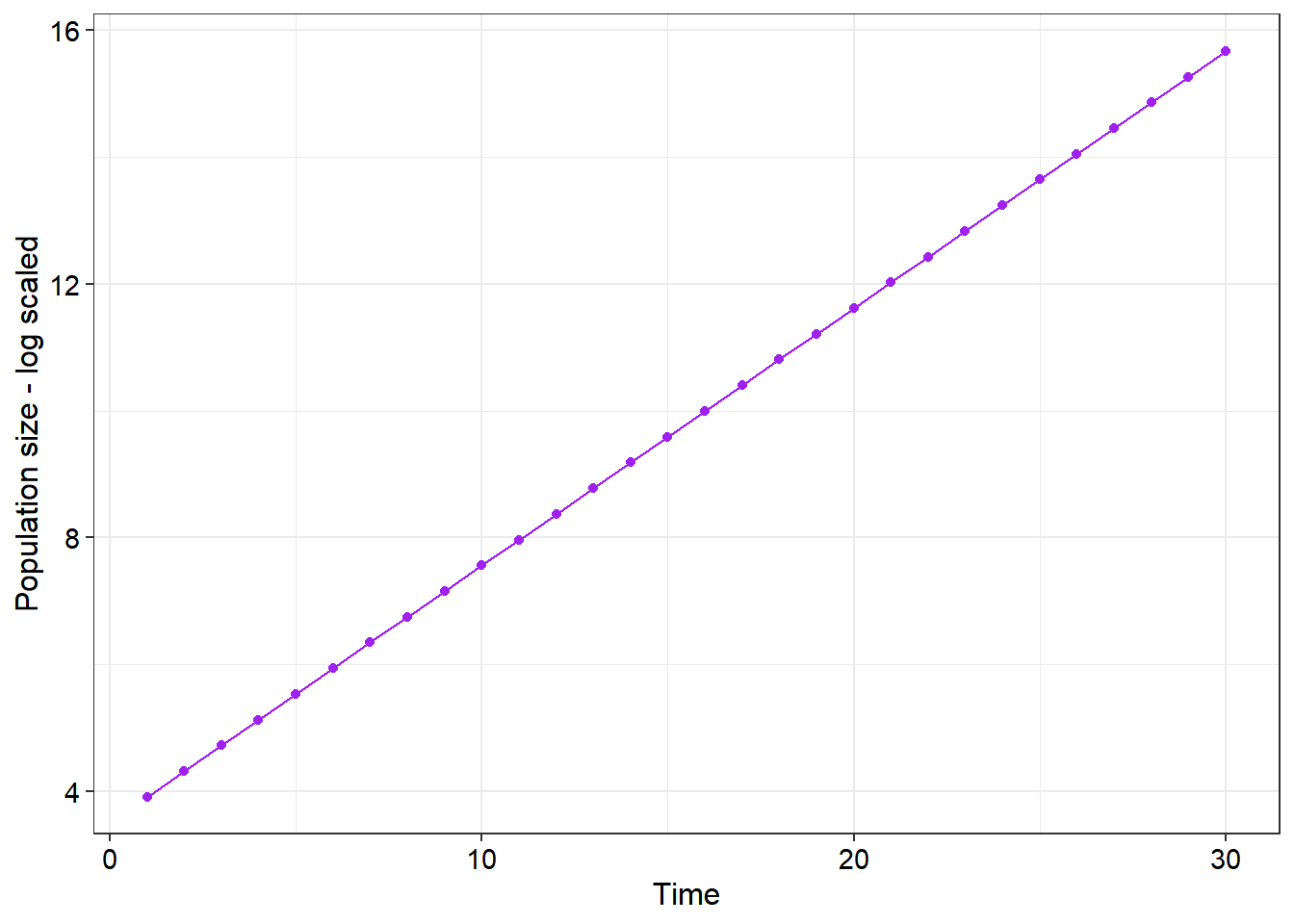
Application questions
- Find three peer reviewed examples where studies have investigated populations growing exponentially and logistically. Give the citation of the paper and the study species. For the three logistically growing populations indicate what environmental factors that the reasearchers linked the carrying capacity to (9)
- Give three factors that could influce both the birth and the survivorship rates (and ultimately \(\lambda\) or \(r\)) for a given population. Give reasons for your answers (6)
- About 160 years ago an alien plant species was introduced to KwaZulu-Natal after a ship carrying a delivery of exotic plants from Mexico to China docked at Port Natal harbour. Trade reports stated that 3 specimens of Lantana camara were sold to a local wealthy family to “beautify” their garden. A recent survey of densities of L. camara in South Africa reported that aprroximately 2 000 000 ha have been invaded by the plant. Assuming that at the time L. camara was introduced into KwaZulu-Natal 1 ha was invaded by the plant, calculate the intrinsic population growth rate between the species’ introduction and the date that the article was published. Show all your working (6)
- Based on the brief discussions in this article what kind of growth pattern (exponential or logistic) do you think L. camara likely demonstrates? (4)
- There are two methods one can use to model population growth. They are discrete and continuous growth. In your own words discuss the theoretical and applied differences of these two methods. You may include examples and references to scientific publications and equations to support your answer (5)